Ewha Womans University Mathematics

 
홈

Research Areas

Prof. Chulkwang Kwak

Analysis and PDE Lab

Faculty Introduction
Prof. Chulkwang Kwak
Prof. Chulkwang Kwak
Research Area
  • Harmonic analysis and Nonlinear dispersive equations
  • Asymptotic models for water waves
Lab Introduction

Analysis helps us to understand in mathematical languages various phenomena arising from the fields of not only mathematical sciences, but also reality. Particularly, nonlinear Partial Differential Equations(PDEs) describes such phenomena, and enables to predict future phenomena based on the study of existence and global dynamics of solutions. In Analysis and PDE Lab, we particularly study theories of well-posedness and long time dynamics of solutions to nonlinear dispersive equations involving asymptotic models for water waves.

Well-posedness theory

This field aims to develop properties of nonlinear solutions from ones of linear solutions investigated by Harmonic analysis technique

Asymptotic dynamics

This field aims to describe global-in-time dynamics of nonlinear solutions based on dispersive properties of solutions and specific structures of equations.

Major research projects and Research achievements
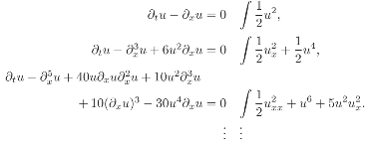
Nonlinear dispersive equations
Nonlinear dispersive equations
  • Local and global well-posedness
  • Continuum limit problems
  • Decay property
Water wave models
Water wave models
  • Asymptotic models
  • Small amplitude limit
  • Long time dynamics
Selected research papers
Mathscinet
Mathscinet
  • (With Hong and Yang) Korteweg-de Vries limiit for the Fermi-Pasta-Ulam system, Arch. Ration. Mech. Anal. 240 (2021), no.2 , 1091-1145.
  • Well-posedness issues on the periodic modified Kawahara equation, Annales de I'lnstitut Henri Poincaré Non Linéaire 37 (2020) 373-416 .
  • (With C. Muñoz) Asymptotic dynamics for the small data weakly dispersive one-dimensional Hamiltonian ABCD system, Transactions of the American Mathematical Society Vol. 373, No. 2, (2020), page 1043 – 1107 .
  • (With C. Muñoz, F. Poblete, and J. C. Pozo) The scattering problem for Hamiltonian ABCD Boussinesq system in the energy space, Journal de Mathématiques Pures et Appliquées, 127 (2019) 121-159 .
  • Local well-posedness for the fifth-order KdV equations on T, Journal of Differential Equations 260, 10, (2016), 7683-7737.