Ewha Womans University Mathematics

 
홈

Research Areas

Prof. Yoonjin Lee

Number Theory and Coding Theory Lab

Faculty Introduction
Prof. Yoonjin Lee
Prof. Yoonjin Lee
Research Area
  • Algebraic Number Theory
  • Algebraic Coding Theory
Lab Introduction

Number Theory and Algebra belong to the major areas of mathematics, and they can be applied to Coding Theory, a part of Information Theory.

We broadly study the arithmetic of function fields and number fields: structure of class groups, non-vanishing of the L-functions over function fields, surjectivity of Galois representations associated with Drinfeld modules, torsion groups of elliptic curves, and so on.

Furthermore, we focus on construction of "good" error-correcting codes, which is one of two major themes of Coding Theory for minimizing the loss of information transmitted through noisy channels. We study a variety of interesting code classes such as self-dual codes, cyclic codes, LCD codes, DNA codes, Quantum codes, Convolutional codes (Turbo codes) and so forth.

Graduate students in this lab currently study the arithmetic of function fields and number fields, a variety of algebraic codes (Self-dual codes, Cyclic codes, LCD codes, Convolutional codes, and etc) and cryptographic functions (bent functions, plateaued functions).

Major research projects and Research achievements
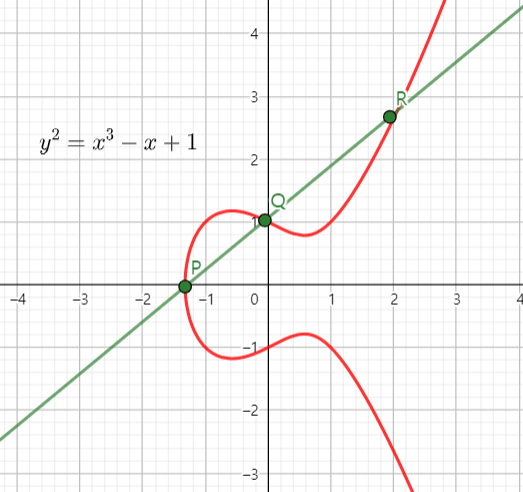
Algebraic Number Theory
Number Theory
  • Arithmetic of number fields and function fields
  • Arithmetic of Drinfeld modules
  • Structure of ideal (or divisor) class groups of global function fields and number fields
  • Non-vanishing of L-functions for various characters in function fields
  • Modularity of various types of continued fractions
  • Torsion group structure of elliptic curves and hyperelliptic curves
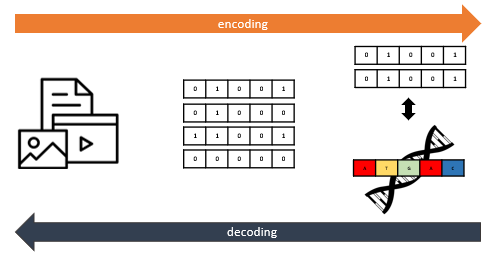
Algebraic Coding Theory
Algebraic Coding Theory
  • Self-dual codes, Formally self-dual codes
  • Cyclic codes, Quasi-cyclic codes
  • Algebraic Geometric codes and Number field codes
  • Convolutional codes, LCD codes, DNA codes
  • Cryptographic functions: Bent functions and Plateaued functions
  • Strongly regular graphs, Few-weight codes
Selected research papers
Mathscinet
Mathscinet
  • J. Lee, Y. Lee, Non-vanishing of L-functions for cyclotomic characters in function fields, To appear in Proc. Amer. Math. Soc., 2021 (accepted for publication)
  • J. Yoo, Y. Lee, Infinite families of cyclic function fields with prescribed class group rank, Journal of Pure and Applied Algebra, vol. 225 (2021), no. 9, 106658.
  • W.-H. Choi, H. J. Kim, Y. Lee, Construction of single-deletion-correcting DNA codes using CIS codes, Designs, Codes and Cryptography, vol. 88 (2020), No. 12, 2581-2596.
  • J. Y. Hyun, J. Lee, Y. Lee, Infinite families of optimal linear codes constructed from simplicial complexes, IEEE Transactions on Information Theory, Vol. 66, (2020), No. 11, 6762-6773.
  • H. J. Kim, W.-H. Choi, Construction of reversible self-dual codes, Finite Fields and their Applications, vol. 67 (2020), 101714.
Graduate Students
  • Nayoung Han  Ph. D student
    Research Area: algebraic coding theory, convolutional codes
  • Jihye Jeong Ph. D student
    Research Area: algebraic coding theory, cryptographic functions
  • Siyun Lee Ph. D student
    Research Area: number theory, arithmetic of number fields
  • Shin-Yoo Park Master's student
    Research Area: algebraic coding theory
  • Woojung Choi Master's student
    Research Area: algebraic coding theory