이화여자대학교 수학과

 
홈

연구분야소개

이윤진

정수론 및 부호 이론 연구실 (Number Theory · Coding Theory Lab)

교수진 소개
이윤진 교수
이윤진 교수
연구 분야
  • Algebraic Number Theory
  • Algebraic Coding Theory
연구실 소개

대수학(Algebra) 및 정수론(Number Theory) 분야는 순수 수학의 중심 분야일 뿐만 아니라 부호 이론(Coding Theory) 등 정보 이론 분야에 활발하게 응용 되고 있는 주요 학문 분야이다. 본 연구실에서는 대수적 방법론을 이용하여 대수적 수체(Number Field)와 함수체(Function Field)의 산술(Arithmetic) 및 부호 이론 분야의 대수 기반 코드(Algebraic Code), 대수 기하 코드(Algebraic Geometry Code) 등에 관해 연구하고 있다.

대수학(Algebra) 및 정수론(Number Theory) 분야 연구

대수적 수체(Number Field)와 함수체(Function Field)의 산술(Arithmetic) 에 관하여 연구하고 있다. 수론 분야의 매우 중요한 불변량인 수체 및 함수체의 Class group의 구조에 관한 연구를 활발히 진행하고 있으며 특히, Cyclotomic 수체 및 함수체의 Class group 구조를 연구하고 있다. 또한, 함수체 위에서 정의된 L-function의 non-vanishing을 연구하고 Drinfeld module에 연계된 Galois representation의 surjectivity 및 타원곡선의 torsion group 구조를 연구한다.

부호 이론(Coding Theory) 분야 연구

부호 이론은 통신 채널에서 정보의 손실을 최소화하는 정보 전송 방법을 연구하는 분야로, 특히 부호이론은 대수학 및 정수론에 기반하여 효율적인 정보 전송 방법 및 저장 방법(Data Storage)에 대해 연구하는 분야이다. 전송하려는 정보의 종류 및 통신 환경에 따라 Self-dual code, Cyclic code, LCD code, DNA code, Quantum code, Convolutional code (Turbo code) 등 다양한 종류의 코드 생성방법론을 활발하게 연구하고 있다.

주요 연구 프로젝트 및 연구 업적
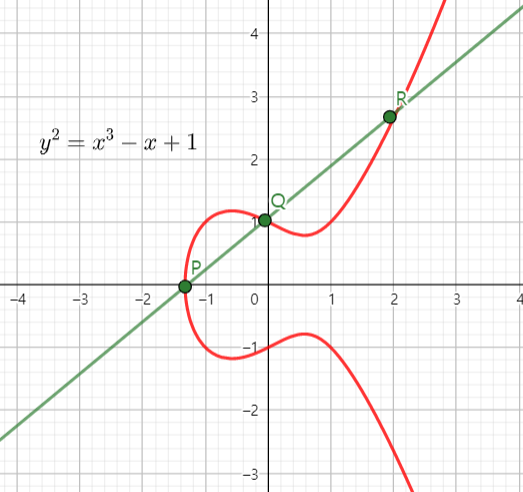
Algebraic Number Theory
Algebraic Number Theory
  • Arithmetic of number fields and function fields
  • Arithmetic of Drinfeld modules
  • Structure of ideal (or divisor) class groups of global function fields and number fields
  • Non-vanishing of L-functions for various characters in function fields
  • Modularity of various types of continued fractions
  • Torsion group structure of elliptic curves and hyperelliptic curves
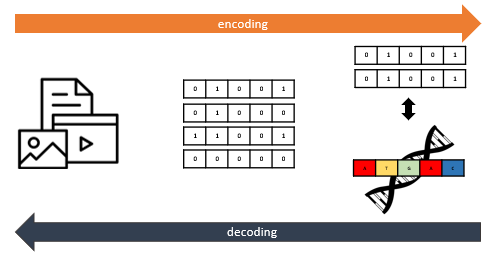
Algebraic Coding Theory
Algebraic Coding Theory
  • Self-dual codes, Formally self-dual codes
  • Cyclic codes, Quasi-cyclic codes
  • Algebraic Geometric codes and Number field codes
  • Convolutional codes, LCD codes, DNA codes
  • Cryptographic functions: Bent functions and Plateaued functions
  • Strongly regular graphs, Few-weight codes
주요 연구 논문 (selective list)
Mathscinet
Mathscinet
  • J. Lee, Y. Lee, Non-vanishing of L-functions for cyclotomic characters in function fields, To appear in Proc. Amer. Math. Soc., 2021 (accepted for publication)
  • J. Yoo, Y. Lee, Infinite families of cyclic function fields with prescribed class group rank, Journal of Pure and Applied Algebra, vol. 225 (2021), no. 9, 106658.
  • W.-H. Choi, H. J. Kim, Y. Lee, Construction of single-deletion-correcting DNA codes using CIS codes, Designs, Codes and Cryptography, vol. 88 (2020), No. 12, 2581-2596.
  • J. Y. Hyun, J. Lee, Y. Lee, Infinite families of optimal linear codes constructed from simplicial complexes, IEEE Transactions on Information Theory, Vol. 66, (2020), No. 11, 6762-6773.
  • H. J. Kim, W.-H. Choi, Construction of reversible self-dual codes, Finite Fields and their Applications, vol. 67 (2020), 101714.
대학원생 소개
  • 한나영 박사과정생
    연구분야: algebraic coding theory, convolutional codes
  • 정지혜 박사과정생
    연구분야: algebraic coding theory, cryptographic functions
  • 이시윤 박사과정생
    연구분야: number theory, arithmetic of number fields
  • 최우정 석사과정생
    연구분야: algebraic coding theory